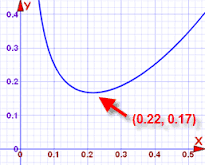
- modello aritmetico, in cui si utilizza una rappresentazione mediante tavole delle operazioni, vettori, gruppi;
- modello algebrico-analitico, ossia il modello rappresentato da determinate tipologie di equazioni o disequazioni, o equazioni o sistemi di disequazioni, con variabili che possono essere di diversa natura;
- modello grafico, rappresentato dal grafico che esprime una determinata dipendenza funzionale;
- modello geometrico, rappresentato mediante figure geometriche;
- modello combinato.
La scelta di un modello e quindi della rappresentazione matematica dipende dalle caratteristiche della situazione problematica che si intende modellizzare e dalle informazioni date come input.
Per creare un modello matematico è necessario quindi sviluppare delle precise competenze da affinare nell’arco del corso di studi.
Il termine competenza indica la comprovata capacità di usare conoscenze, abilità e capacità
personali, sociali e/o metodologiche, in situazioni di lavoro o di studio e nello sviluppo
professionale e/o personale; le competenze sono descritte in termine di responsabilità e autonomia.
Quindi una competenza può essere intesa come l’insieme di tutte le conoscenze, abilità e attitudini acquisite nell’arco della propria vita e che consentono a ogni persona di agire nella maniera più adeguata per affrontare una determinata situazione problematica in qualsiasi contesto.
Le competenze chiave, invece, sono quelle competenze che vengono utilizzare in diversi campi di attività e rappresentano solo una parte di tutte le conoscenze, abilità e attitudini acquisite nell’arco della propria vita.
Alla luce di quanto detto, le competenze relative al processo della modellizzazione matematica sono le seguenti:
- concentrarsi sui punti di partenza del modello situazione,
- strutturare le situazioni da modellizzare,
- “matematizzare” il modello (trasferimento della “realtà” nelle idonee strutture matematiche), cioè produrre delle relazioni quantitative tra le variabili individuate come fondamentali,
- costruire modelli matematici,
- dimostrare che il modello è coerente con la situazione reale,
- analizzare il modello,
- presentare il modello (compresi le situazioni limite e le limitazioni),
- “dematematizzare” il modello, ossia interpretare il modello utilizzando i termini della vita quotidiana,
- controllare tutto il processo di modellazione.