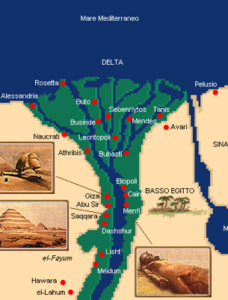
Sfondo storico dell’Egitto
Non sono note le origini della civiltà egiziana, ma questo popolo esisteva già prima del 4000 a.C. Erodoto definiva l’Egitto un dono del Nilo: il fiume scorre da nord a sud e straripava una volta all’anno, lasciando una sostanza fertilissima chiamata limo.
Il periodo di maggior splendore si ebbe durante la terza dinastia (2500 a.C.), infatti proprio in questo periodo furono costruite le piramidi.
La civiltà egiziana si sviluppò fino al 332 a.C, anno in cui Alessandro Magno conquistò l’Egitto. Il popolo degli Egiziani venne a contatto con la sola civiltà degli Hyksos, i quali invasero l’Egitto tra il 1700 e il 1600 a.C.
Gli Egizi inventarono la scrittura geroglifica, utilizzata nei monumenti fino all’inizio dell’era cristiana; inoltre, dal 2500 a.C., utilizzarono la scrittura ieratica, che risulta sillabica perché una parola è costituita dall’associazione di due ideogrammi.
I più importanti papiri egiziani pervenutici, risalenti al 1700 a.C. circa, sono:
- Papiro di Mosca, conservato a Mosca;
- Papiro di Rhind, conservato al British Museum di Londra.
I contributi matematici degli Egizi sono stati studiati grazie alla traduzione della scrittura cuneiforme.
Nel 1870, dopo la scoperta della roccia di Behistun che presentava una scrittura trilingue sulla vittoria di Dario su Cambise, fu possibile interpretare il babilonese antico, lingua affine all’assiro e nota grazie alla sua traduzione in lingua persiana.
La scoperta della Stele di Rosetta (1799) nel corso della spedizione napoleonica permise la traduzione del geroglifico, in quanto essa era scritta in greco, demotico e geroglifico. Grazie a ciò fu possibile scoprire il sistema di numerazione in base 10 egiziano che risale a 5000 anni fa circa.
Gli Egiziani scrivevano le cifre piccole a sinistra e qualche volta le disponevano verticalmente; i simboli ogni tanto venivano disposti al contrario.
Questo popolo aveva raggiunto un alto livello di precisione nel contare e nel misurare, ne è prova la loro capacità di costruire piramidi.
Anche se sono pervenuti documenti cerimoniali, astronomici e pietre tombali, le vere informazioni sul sapere matematico degli Egizi ci vengono dai suddetti papiri.
Caratteristiche del Papiro di Rhind
- È largo 30 cm e lungo 5,46 cm circa.
- È conservato al British Museum di Londra (alcuni frammenti si trovano presso il Museo di Brooklyn).
- Fu acquistato nel 1858 dall’antiquario scozzese Henry Rhind presso una città balneare sul Nilo.
- È noto anche come papiro di Ahmes, dal nome dello scriba che lo trascrisse nel 1650 a.C. Per tale ragione si pensa che Ahmes sia stato uno dei primissimi matematici dell’antichità.
- È scritto utilizzando la scrittura ieratica (sacra) e non demotica (popolare).
- La numerazione in esso presente è decimale, ma è anche possibile ritrovare cifre e segni speciali per i numeri da 1 a 9 e i multipli delle potenze di 10.
L’aritmetica egizia
Era prevalentemente additiva e, di conseguenza, la moltiplicazione e la divisione venivano ricondotte a procedimenti di natura additiva.
L’algebra egizia
Nei papiri sono contenuti problemi a un’incognita. Tali problemi facevano parte dell’aritmetica, infatti non si parla ancora di una vera e propria algebra.
I problemi erano enunciati verbalmente insieme alle operazioni utili per la loro risoluzione. Per esempio, nel papiro di Rhind, il problema 31 è espresso come segue: «una quantità, i suoi 2/3, il suo ½, il suo 1/7, il suo intero equivale a 33».
Oggi tradurremmo questo problema mediante l’equazione:
$$\frac{2}{3}x+\frac{1}{2}x+\frac{1}{7}x+x=33$$
La geometria egizia
Il popolo degli Egizi considerava la geometria non separata dall’algebra e, così come i babilonesi, la consideravano una disciplina pratica. Infatti, applicavano l’algebra e l’aritmetica al calcolo delle aree e dei volumi.
Secondo Erodoto la geometria egiziana nacque dall’esigenza di rideterminare annualmente i confini dei campi cancellati dallo straripamento del Nilo.
Gli Egizi sapevano calcolare le aree dei triangoli, dei quadrati e dei trapezoidi. Calcolavano l’area del cerchio mediante la relazione:
$$A=\left( \frac{8}{9} d \right)^2$$
con d diametro. La formula era abbastanza veritiera, in quanto equivaleva ad utilizzare il numero 3,1605 anziché 3,1415.
Inoltre, sapevano calcolare il volume del cubo, del parallelepipedo e del cilindro e utilizzavano la forma usata oggi per il calcolo del volume del tronco di cono a base quadrata:
$$V=\frac{h}{3} \left( a^2+ab+b^2 \right)$$
La prova della loro bravura geometria è possibile notarla nelle tre piramidi di Giza che costruirono tra il 2700 e il 2500 a.C. Esse erano le tombe dei faraoni Cheope, Chefren e Micerino e avevano i quattro spigoli rivolti verso i punti cardinali per ragioni di natura religiosa.
Applicazioni della matematica egiziana
- Determinazione dei salari dei lavoratori
- Determinare i volumi dei granai
- Determinare le aree dei campi da coltivare
- Ripartire equamente le tasse in base all’estensione dei terreni
- Calcolare il numero di mattoni per la costruzione di un edificio
- Compilazione di un calendario per le attività commerciali e per predire le feste religiose
- Astronomia
- Stima dell’anno solare
- Costruzione di templi in posizione tale che il sole li colpisse in un determinato modo, così anche le piramidi e le sfingi che erano rivolte ad est
Riassumendo
- Formularono l’aritmetica degli interi e delle frazioni
- Posero le basi rudimentali dell’algebra
- Utilizzarono alcune formule geometriche empiriche
- È assente il simbolismo matematico
- Sono assenti le dimostrazioni matematiche
- Sono considerati i carpentieri della matematica, mentre i Greci sono i cosiddetti architetti della matematica